2270. Поиск цикла
Дан ориентированный невзвешенный граф. Определите, содержит ли он циклы. Если граф содержит цикл, выведите любой
из них.
Вход. В первой строке находятся два натуральных числа n, m
(1 ≤ n ≤ 105,
1 ≤ m ≤ 105) –
количество вершин и ребер в графе соответственно. В следующих m строках перечислены рёбра графа. Каждое ребро задаётся
парой чисел – номерами начальной и конечной вершины.
Выход. Если в графе
цикла нет, выведите строку “NO”. Если цикл существует,
выведите строку “YES”, и затем перечислите вершины, входящие в цикл, в порядке их
обхода. Если циклов существует несколько, выведите любой.
|
Пример
входа 1 |
Пример
выхода 1 |
2 21 2
2 1 |
YES 1 2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
6 7 1 2 2 3 2 4 4 6 6 5 1 5 5 2 |
YES 2 4 6 5 |
РЕШЕНИЕ
графы –
поиск в глубину
Анализ алгоритма
Выполним серию
обходов графа в глубину. Для этого из каждой вершины, в которой мы ещё не были,
запустим поиск в глубину. При входе в вершину будем окрашивать её в серый цвет,
а при выходе – в чёрный. Если во время поиска мы попытаемся перейти в вершину,
уже окрашенную в серый цвет, это будет означать, что найден цикл.
Для
восстановления цикла необходимо сохранять последовательность вершин в порядке
их обхода. Например, если массив обхода содержит вершины (2, 6, 3, 5, 4, 3), то
искомым циклом будет (3, 5, 4).
Пример
Графы, приведенные
в условии задачи, имеют следующий вид:
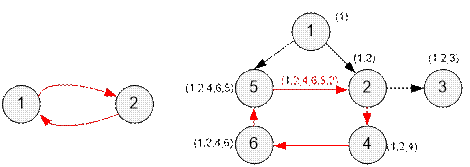
Возле каждой вершины
указано текущее состояние массива path.
Реализация алгоритма
Список смежности
графа хранится в векторе g. В массиве
path сохраняем
последовательность вершин в порядке обхода в глубину.
vector<vector<int> > g;
vector<int> used, path;
Функция dfs реализует поиск
в глубину из вершины v. При входе в
вершину v окрашиваем её в серый цвет (used[v] = 1), а при выходе
– в черный (used[v] = 2). Глобальная переменная flag указывает на наличие
цикла: flag = 1 означает, что цикл
найден, flag = 0 означает, что цикла нет.
void dfs(int
v)
{
Если цикл уже был найден (flag = 1), продолжать поиск смысла нет.
if
(flag == 1) return;
Вершину v отмечаем серой и
добавляем в массив path.
used[v] = 1;
path.push_back(v);
Перебираем вершины to, смежные с v.
for (int to : g[v])
Цикл считается найденным, если поиск
в глубину старается пойти в серую вершину (в вершину to, для которой
used[to] = 1).
if
(used[to] == 1)
{
path.push_back(to);
flag = 1;
return;
}
Если вершина to еще белая, продолжаем из нее
поиск в глубину.
{
if (used[to] == 0) dfs(to);
if (flag == 1) return;
}
После завершения обработки вершины v отмечаем её чёрным цветом. Удаляем вершину v из
массива path.
used[v] = 2;
path.pop_back();
}
Основная часть программы. Читаем список
ребер и строим список смежности графа.
scanf("%d %d", &n, &m);
g.resize(n + 1);
used.resize(n + 1, 0);
for(i = 0; i < m; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
}
Запускаем серию обходов в глубину.
Если вершина i еще не обработана
(used[i] = 0), запускаем из нее поиск в глубину. Если при
выполнении очередного вызова функции dfs
значение переменной flag становится равной 1
(обнаружен цикл в графе), прекращаем дальнейший поиск.
for (i = 1; i <= n; i++)
if
(used[i] == 0)
{
dfs(i);
if
(flag == 1) break;
}
Если flag = 1, это означает, что цикл был
найден. В таком случае выводим его, исходя из
информации в массиве path.
if (flag == 1)
{
Цикл найден и завершается
в вершине cfin =
path[path.size() – 1].
Двигаемся переменной cstart назад
по массиву path, чтобы найти ту же вершину cfin – точку, в
которой начинается цикл.
while (path[cstart] != cfin) cstart--;
Выводим сообщение о наличии цикла и сам цикл.
printf("YES\n");
for (i = cstart; i <
path.size() - 1; i++)
printf("%d ", path[i]);
printf("\n");
}
Иначе (flag = 0) циклов
в графе нет.
else printf("NO\n");
Java реализация
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static int used[], flag, n, m;
static Vector<Integer> path = new
Vector<Integer>();
static void dfs(int v)
{
if (flag == 1) return;
used[v] = 1;
path.add(v);
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == 1)
{
path.add(to);
flag = 1;
return;
}
else dfs(to);
if (flag == 1) return;
}
used[v] = 2;
path.remove(path.size() - 1);
}
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new ArrayList[n+1];
for (int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
used = new int[n+1];
for(int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
}
for (int i = 1; i <= n; i++)
if (used[i] == 0)
{
dfs(i);
if (flag == 1) break;
}
if (flag == 1)
{
int i = path.size() - 2;
int to = path.lastElement();
while (path.get(i) != to) i--;
System.out.println("YES");
for (; i < path.size() - 1; i++)
System.out.print(path.get(i) + " ");
System.out.println();
}
else System.out.println("NO");
con.close();
}
}